

 |
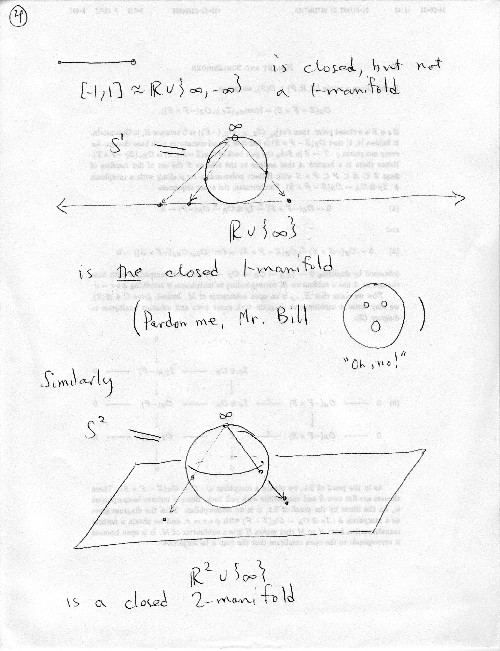
| At the top of page 3 are examples of spaces that are and are not 2-manifolds. An n-manifold is closed if it has no boundary and doesn't go off to infinity. For example, the open interval (-1,1) is not closed: the homeomorphism (a 1-1 and onto map which preserves closeness) given in the picture makes it look like the real line R1 which goes off to infinity. Going to page 4, the interval [-1,1] is closed, but not a 1-manifold. The space S1 (the unit vectors in R2) looks like R1 plus a point at infinity via the stereographic projection map shown with the arrows. Ken told us that S1 is the only closed 1-manifold, which has the Mr. Bill manifold feeling left out. He doesn't count here, because we are considering only connected manifolds here. The same stereographic projection shows that Sn (the unit vectors in Rn+1) can be thought of as Rn plus a point at infinity. The case when n=2 is shown. |