Discrete
Mathematics II Homework
Click here
for solutions to non-book problems
Due Friday Dec. 13 (leave in envelope by
my office in TUC 358B)
Do Additional Exercise 13.9.1, 13.9.4
Due Wednesday Dec. 11
Finish reading 13.9
I. Do Additional Exercises 13.9.2, 13.9.3
II. A zoo wants to set
up natural habitats in which to exhibit its animals. Unfortunately, some
animals will eat some of the others when given the opportunity. How can a graph
model and a coloring be used to determine the number of different habitats
needed and the placement of the animals in these habitats?
III. The mathematics
department has six committees, each meeting once a month. How
many different meeting times must be used to ensure that no member is
scheduled to attend two meetings at the same time? The committees are
C1 = {Arlinghaus, Brand, Zaslavsky}
C2 = {Brand,
Lee, Rosen}
C3 = {Arlinghaus, Rosen, Zaslavsky}
C4 = {Lee,
Rosen, Zaslavsky}
C5 = {Arlinghaus, Brand}
C6 = {Brand,
Rosen, Zaslavsky}
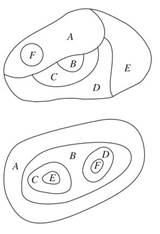
IV. Construct the graphs
associated to the maps shown. Then find the least number of colors needed to
color the map so that no two adjacent regions have the same color.
Due Monday Dec. 9
Read Section 13.9 up to 13.9.2 and do
Participation and Challenge Exercises up through (and including) 13.9.2
1. Do Additional Exercises 13.8.1, 13.8.2,
13.8.3, 13.8.4, 13.8.5
2. Show that if a connected planar graph
with at least 3 vertices has no circuits of length 3 then |E| ≤ 2|V|-4
(hint: modify the proof of Theorem 13.8.2, which we discussed in class)
3. Use the fact of the preceding problem
to give another proof (different from the one from class) that K3,3
is not planar.
4. Suppose that G is a connected k-regular
graph. For what k can you be sure that G is not planar?
Due Friday, December 6
Read Section 13.8 and do all Participation
and Challenge Exercises
I. Do Additional Exercises 13.7.1, 13.7.2,
13.7.3, 13.7.4
II. Note: The book I took the following
problem from calls them “Hamilton circuits” instead of “Hamilton cycles” (why
is that still consistent with our book’s notation?).
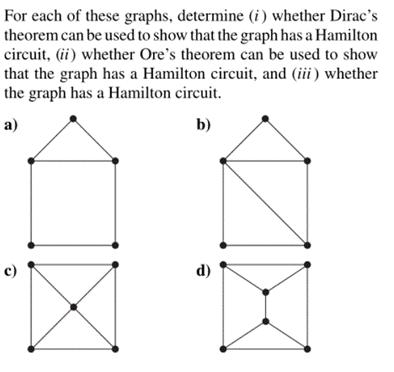
III. Can you find a simple graph with n
vertices with n ≥ 3 that does not have a Hamilton circuit, yet the degree
of every vertex in the graph is at least (n − 1)/2?
Due Wednesday, December 4
Read Section13.6 and do all Participation
and Challenge Exercises
Read Section13.7 and do all Participation
and Challenge Exercises
Do Additional Exercises 13.6.1, 13.6.2,
13.6.3
Due Monday, December 2
Read Section 13.5 and do all Participation
and Challenge Exercises
Do Additional Exercises 13.5.1a, 13.5.2,
13.5.3, 13.5.4
Due Friday, November 22
Do Additional Exercises 13.3.2, 13.3.3,
13.3.4b, 13.4.2, 13.4.4, 13.4.5
Due Wednesday, November 20
Finish reading Section 13.3 and finish all
Participation and Challenge activities
Read Section 13.4 and do all Participation
and Challenge Exercises
Do Additional Exercises 13.2.1, 13.3.1,
13.3.4a
Due Monday, November 18
Read Section 13.2 and do all Participation
and Challenge Exercises
Start reading Section 13.3 and do
Participation Activities up to 13.3.2
1. Do problem 13.1.1.
2. For which values of n is Kn bipartite? Explain your reasoning.
3. For which values of n is Cn
bipartite? Explain your reasoning.
4. Which of the following graphs are bipartite? If the graph is bipartite draw it with a bipartite vertex coloring (i.e. color the vertices of V1 one color and the vertices of V2 a different color). If it is not, explain why not:
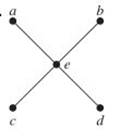
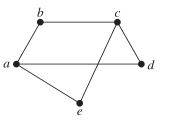
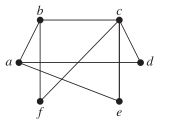
Due Friday, November 15
Read Section 13.1 and do all Participation
and Challenge problems
Do Additional Exercises 8.16.1abgh and
8.16.2cdeg
Due Wednesday, November 13
Finish reading Section 8.16 and do the
remaining Participation and Challenge problems
Do Additional Exercises 8.16.1cdef and
8.16.2abf
Due Monday, November 11
Read Section 8.16 up to Theorem 8.16.1. Do
all Participation and Challenge problems up to 8.16.6
1. Do Additional Exercises 8.15.2bcd,
8.15.3df
2. Find the solution to an = 7an−2
+ 6an−3 with a0 = 9, a1 = 10, and a2
= 32.
Due Friday, November 8
Finish reading Section 8.15 and do
Participation Activities 8.15.6 and 8.15.7
Do Additional Exercises 8.15.1, 8.15.2.a, 8.15.3.abce
Due Wednesday, November 6
Read Section 8.15 except for the section
“Characteristic equations with multiple roots” and do all Participation
activities up through 8.15.5 (8.15.6 and 8.15.7 will be due next time)
Do Additional Exercises 8.2.1, 8.2.2,
8.2.3
Due Monday, November 4
Read Section 8.2 and do all Participation
and Challenge problems
Do Additional Exercises 8.1.1 and 8.1.2
Due Friday November 1
Read Section 8.1 and do all Participation
and Challenge Activities
1. Do Additional Problems 11.3.4, 11.3.5
2. Let (xi ,yi), i =
1,2,3,4,5, be a set of five distinct points with integer coordinates in the xy plane. Show that the midpoint of the line joining at
least one pair of these points has integer coordinates. Hints: What is the
formula for the midpoint? What has to hold for a pair of points for the
midpoint to have integer coordinates?
3. An arm wrestler is the champion for a
period of 75 hours. (Here, by an hour, we mean a period starting from an exact
hour, such as 1 p.m., until the next hour.) The arm wrestler had at least one
match an hour, but no more than 125 total matches. Show that there is a period
of consecutive hours during which the arm wrestler had exactly 24 matches.
Wednesday October 30
Exam 2 – nothing due
Due Monday October 28
Finish reading Section 11.3 and finish the
Participation and Challenge Activities
1. Give Pascal’s triangle up through n=10.
2. What is the coefficient of x3y7
in (x+y)10?
3. Do Additional Exercises 11.3.1, 11.3.2,
11.3.3
Due Friday October 25
Read Section 11.2 and do all Participation
and Challenge Activities; start reading Section 11.3 and working on the
Participation and Challenge Activities (this will be due on Monday)
Do Additional Exercises 10.12.1, 10.12.2,
10.12.3, 11.2.1ab, 11.2.2, 11.2.4b (for part 11.2.4, prove the identity
by showing that the left and right sides correspond to counting the same thing
in two different ways)
Due Wednesday October 23
Do Additional Exercises 10.10.4, 10.10.5,
10.10.6, 10.11.1, 10.11.4, 10.11.5
Due Monday, October 21
Read Sections 10.11 and 10.12 and do all
Participation and Challenge Activities
Do Additional Exercises 10.9.1, 10.9.2,
10.9.3, 10.9.4, 10.9.6, 10.10.1, 10.10.2, 10.10.3
Due Friday, October 18
Read Sections 10.9 and 10.10 and do all
Participation and Challenge Activities
Do Additional
Exercises 10.7.1, 10.7.2, 10.7.3, 10.7.4, 10.8.1, 10.8.2, 10.8.3, 10.8.4,
10.8.7
Due Monday, October 14 Wednesday,
October 16
Read Sections 10.7 and 10.8 and do all
Participation and Challenge Activities
1. Do
Additional Exercises 10.6.1-10.6.6. Note that in problems 2, 3, and 4 you can
assume that the choices from part a are already fixed for later parts of the
problem. For example, in 10.6.3, the 12 players have already been decided in
part a.
2. Suppose the Math Department has 15 professors, the Computer
Science Department has 10 professors, and the Engineering Department has 12
professors. How many ways are there to form a committee of 7 by choosing 3
professors from one of the departments and 2 from each of the others?
Due Friday, October 11
Read Section 10.5 and do all Participation
and Challenge Activities
Do Additional Exercises 10.5.2, 10.5.3,
10.5.4, 10.5.5, 10.5.6, 10.5.7, 10.5.8
Due Monday, October 7
Read Section 10.5 and do all Participation
and Challenge Activities
Do Additional Exercises 10.4.1, 10.4.2,
10.4.3, 10.4.4
Due Friday, October 4
Read Section 10.4 and do Participation and
Challenge Activities
Do Additional Exercises
1. 10.2.1, 10.2.2, 10.2.3, 10.2.4, 10.2.5 (note that for
several of these problems there is proving to be done to show that your
function is bijective – in particular, you must prove it is surjective and
injective)
2. Consider a 3x3x3 cube (like a Rubik’s cube). Three ants named
Abigail, Bobbie, and Cliff have decided to live in the cube, each in their own
1x1x1 cell, but they don’t want any of their coordinate addresses to be the
same. In other words no two can share the same x
coordinate, y coordinate, or z coordinate for their cell. So, for example, if
one ant lives in the top face of the cube, then no other ant can live in the
top face. They don’t like to look at each other. How many ways are there for
the ants to live in the cube? (Note: you can tell the ants apart. You can also
assume you can tell the cube locations apart, so symmetry of the cube doesn’t
matter.)
3. Abigail, Bobbie, and Cliff have moved out of the cube from the
last problem, and three indistinguishable termites have moved in. How many ways
are there to put the termites in the cube so that no two share a coordinate,
recognizing that once they’re in there you can’t tell them apart.
Due Wednesday, October 2
1. Do Additional Exercises 10.2.2, 10.2.3, 10.2.4
2. This problem was added on Thursday a bit after the others: This
problem is intended to better illustrate a point from class on Wednesday,
September 25.
a.
Suppose a class has 18 men and 18 women.
The class will elect three class officers: President, Vice-President, and
Treasurer. No person can hold more than one of these positions. The President
and Treasurer must be the same gender. The President and Vice President must be
different genders. How many ways can the officers be chosen?
b. Suppose
the class instead has 17 men and 18 women. How many ways can the officers be
chosen now? Hint: the generalized product rule will not work for this problem
(think carefully about why).
Due Friday, September 27
Read 10.2 and do the Participation
Activities up through activity 10.2.2.
1. Do Additional Exercises 10.3.1, 10.3.2,
10.3.3, 10.3.4
2. How many injective (one-to-one)
functions are there from a set with m elements to a set with n elements?
Due Wednesday, September 25
Read Section 10.3 and do all Participation
and Challenge Exercises
1. Do Additional Exercises 10.1.1, 10.1.2
2. There are 18 mathematics majors and 325
computer science majors at a college.
a) In how many ways can two representatives be picked so that one
is a mathematics major and the other is a computer science major?
b) In how many ways can one representative be picked who is either
a mathematics major or a computer science major?
3. A multiple-choice test contains 10
questions. There are four possible answers for each question.
a) In how many ways can a student answer the questions on the test
if the student answers every question?
b) In how many ways can a student answer the questions on the test
if the student can leave answers blank?
Due Monday, September 23
Read Section 10.1 and do all Participation
and Challenge exercises.
I. Do Additional Exercises 6.9.1, 6.9.2,
6.9.3ab
II. Consider the equivalence relation on
the real numbers from class with R = {(x,y)
| x − y is an integer}.
a) What is
the equivalence class of 1 for this equivalence relation?
b) What is
the equivalence class of 1/2 for this equivalence relation?
II. In class and in the text, you have
seen that an equivalence relation on a set A determines a partition of A.
Prove the converse: given a partition of A
into pairwise disjoint subsets A1, A2,…,An,
define an equivalence relation on A whose equivalence classes are the given
subsets Ai. (Hint: your relation won’t be given in general by any
kind of algebraic or arithmetic formula, rather you should describe in words
how to tell if two elements of A are related.)
Due Friday, September 20
Read Section 6.9 and do all Participation
and Challenge Exercises.
Do Additional Exercises 6.7.1, 6.7.2.abcd, 6.8.1.de (prove the needed properties), 6.8.4
Due Wednesday, September 18
Finish reading Section 6.7 and doing Participation and
Challenge Exercises.
Read Section 6.8 and do all Participation
and Challenge Exercises.
1. Which of these relations on the positive integers are partial orders?
Which of the partial orders are total orders?
You don’t have to verify the properties by hand, but if something is not a
partial order or total order, explain why by giving a property that is missing.
a) aRb if a=b
b) aRb if a≠b
c) aRb if a≥b
d) aRb if a<b
e) aRb if b=an for some
integer n≥1
2. Which of the following graphs labeled
9, 10, 11 show partial orders. Note that 11 has “two pieces”?
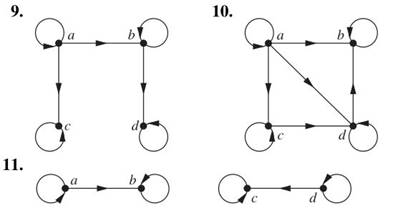
3. Which of these pairs of elements are
comparable in the poset given by the integers with aRb if a divides b?
a) 5,15
b) 6,9 c) 16, 8
d) 7,7
4. Let Z denote the integers. Sort the
following elements of Z×Z into the lexicographic order determined by the total
order ≤ on Z:
(1,3) (2,4), (-2,3), (1,1), (2,6)
Due Monday, September 16
Start reading Section 6.4 and doing
Participation and Challenge Exercises. The full section will be due on 9/18
1. Do Additional Exercises 6.5.1, 6.5.2,
6.5.3, 6.5.4
2. Consider the relation on the real
numbers such that xRy if and only if |x-y|≤2.
Describe R+. You do not have to provide a proof.
3. Let R be a relation on a set A.
a. Say
precisely what it means for xR+y to be
true in terms of powers of R.
b. Prove that
R+ is transitive.
c. Prove that
R+ is the smallest transitive relation on A that contains R. In
other words, show that if S is another transitive
relation on A such that R![]() S then R+
S then R+![]() S. This shows that any other way of extending R to be a transitive
relation must include R+.
S. This shows that any other way of extending R to be a transitive
relation must include R+.
Due Friday, September 13
Read Section 6.5 and do all Participation and
Challenge activities
Note the hyperlinks in some of these
problems.
1. Do Additional Exercises 6.4.1 and
6.4.2. For 6.4.2, make sure to provide your arguments.
2. If R is the relation on the real
numbers with xRy if and only if |x-y|≤2, show
that xR2y if and only if |x-y|≤4. Provide a detailed proof.
Hint: you will need to use the triangle
inequality.
3. Read this
argument that proves the theorem we discussed in class (this is a more
official write-up of what I presented in class).
4. Prove that if R is reflexive and
transitive then Rn=R for all n≥1. You may use the theorem from
class as part of your proof.
5. Show that if R is reflexive then so is
Rn for all n≥1. Hint: use induction.
6. Suppose that R is antireflexive. Must R2
be antireflexive? Why or why not?
Due Wednesday, September 11
Read Section 6.4 and do all Participation and Challenge Activities
Do Additional Exercises 6.3.1, 6.3.2,
6.3.3
Due Monday, September 9
Read Section 6.3 and do all Participation and Challenge Activities
1. Do Additional Exercises 6.2.1.ijl
2. Give an example of a single relation that is all of the
following: reflexive, symmetric, and transitive.
3. A relation R is called asymmetric
if (a,b)ϵR implies that (b,a) is not in R. Give an example of an asymmetric relation
on a non-empty set.
4. Must an asymmetric relation be antisymmetric? Must an
antisymmetric relation be asymmetric? Give reasons for your answers.
Due Friday, September 6: NOTE – SOME PROBLEMS THAT WERE ORIGINALLY
DUE ON 9/6 HAVE BEEN MOVED TO 9/9
Do Additional Exercises 6.2.1.cdefgh,
6.2.3 – note the instruction for 6.2.1 to
justify your answers. For your justifications, you may use the observation from
class that a relation cannot be both reflexive and anti-reflexive unless the
set has no elements.
No additional reading assignment
Due Wednesday, September 4: Read Section 6.2 and do all
Participation and Challenge Activities
Due Wednesday, September 4:
I.
List the ordered pairs in the relation R from A = {0,1,2,3,4} to B = {0,1,2,3},
where (a,b) ∈ R if and only if
a) a = b
b) a + b = 4
c) a > b
d) a | b
II. Do Additional Exercises
6.1.1 and 6.1.2. When asked to draw diagrams, for relations on two different
sets draw the type of diagram with two columns and for relations on a single
set draw a digraph.
Due Friday August 25: Read Section 6.1 and do all Participation
and Challenge Activities
Due Friday, August 25: Review Assignment – if there are concepts
in these assignments with which you are not familiar, make sure to look them up
in the book, read about them, and do the Participation Activities. Note, the following numbers all refer to
the “Addition Exercises,” not the “Participation Activities.”
I. Do the following “additional exercises” in the on-line book: 1.2.1abcd, 1.3.2a, 1.4.5a, 1.6.2(a-f), 1.8.2ac (just provide an English sentence stating the negation, though you may use the logical expressions as a tool if that helps you get your answer), 1.9.3abfgh
II. Do the following “additional exercises” in the on-line book: 2.1.1abc, 2.1.3ab, 2.2.1a, 2.2.2a, 2.2.4ac, 2.3.1a
III. Do the following “additional exercises” in the on-line book: 3.1.1abdeg, 3.1.2abce, 3.3.1acd
IV. Do the following “additional exercises” in the on-line book: 4.1.1, 4.1.3, 4.3.1ac, 4.3.2abcef, 4.4.2abc, 4.5.1abcd, 4.5.2e, 4.5.4ab